课程简介
数学是什么？数学是数字也是图形，是汗水也是灵感，是规则也是想象。这门课将通过一系列精心选取的问题，带初学者领略数学世界风光的同时，也体会劳作的必要。可以把这门课理解为一次徒步之旅。
本课程的目标是将学生对数学的认识从解决问题过渡为认识原理。包括的主要内容为计数法、数域的扩展、数的运算规则等。
内容
- 关于数
- 关于图形
- 关于猜
- 关于抽象
- 排列组合初步
课本
- Arithmetic, P. Lockhart
-
讲义
建议学生程度
五年级和六年级
代数I
课程简介
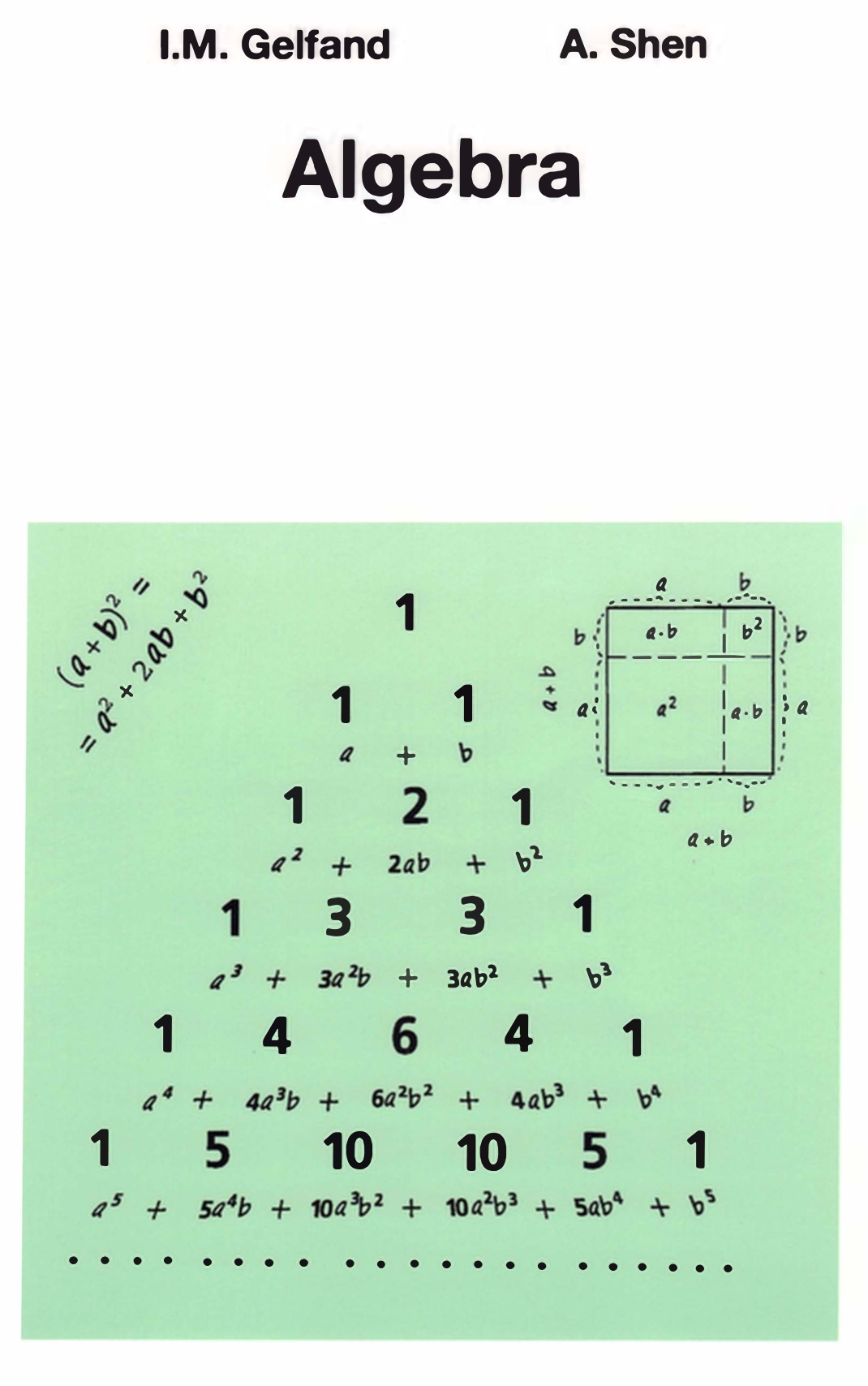
除了学科内容，本课程的主要目的是帮助同学完成从小学向初中的转向。首先是学习内容的转向，小学数学以算术为主，强调对数字的认识和运算。初中开始学习代数，学生会第一次接触符号运算以及抽象的运算规则。学生需要在思维方式上有所成长，以应对内容的变化。抽象思维对这个年龄的学生而言，一开始可能是相当别扭的。理想情况下，我们希望比较和缓地引导学生完成这种转向。从这个目的出发，课程内容的编排将比较灵活，尽量保持课程的趣味性。
本课程将从直观实际的角度理解数域从自然数->整数->有理数->实数的扩展过程。掌握一些基本的代数工具，如多项式和数列等。理解函数的直观概念，以及方程与函数的关系，可以用相关概念和方法解决实际问题。通过对这些基本数学概念的学习了解代数的思考方式，了解抽象的能力与必要。材料上这门课覆盖了普通学校初中绝大部分代数内容。
内容
- 数和数的运算规则
- 二项式展开
- 多项式和数列
- 一次方程
- 二次方程与二次不等式
课本
- Algebra, I. M. Gelfand and A. Shen
- Basic Mathematics, Serge Lang
建议学生程度
七年级
几何I
课程简介
熟悉基本的几何对象，如三角形和圆，熟悉和掌握这些几何对象的性质。以欧几里得几何为实例了解一个逻辑体系的建立过程。通过很多有趣的具体问题了解几何的思考方式。材料上这门课覆盖了普通学校初中几何全部内容。
内容
- 直线
- 圆
- 相似
- 多边形
- 面积
课本
- Kiselev’s Geometry Book 1, A. Kiselev
建议学生程度
六年级
几何II
课程简介
这门课的主题是解决几何问题。通过多个专题的训练增强学生对几何的具体感受，培养学生直观思维的能力。许多巧妙的几何问题将激发学生一方面对几何，另一方面对思维方式的兴趣。
内容
数十个几何专题，包括三角形、四边形、圆、面积等。
课本
- Geometry in Problems, A. Shen
建议学生程度
八年级
代数II
课程简介
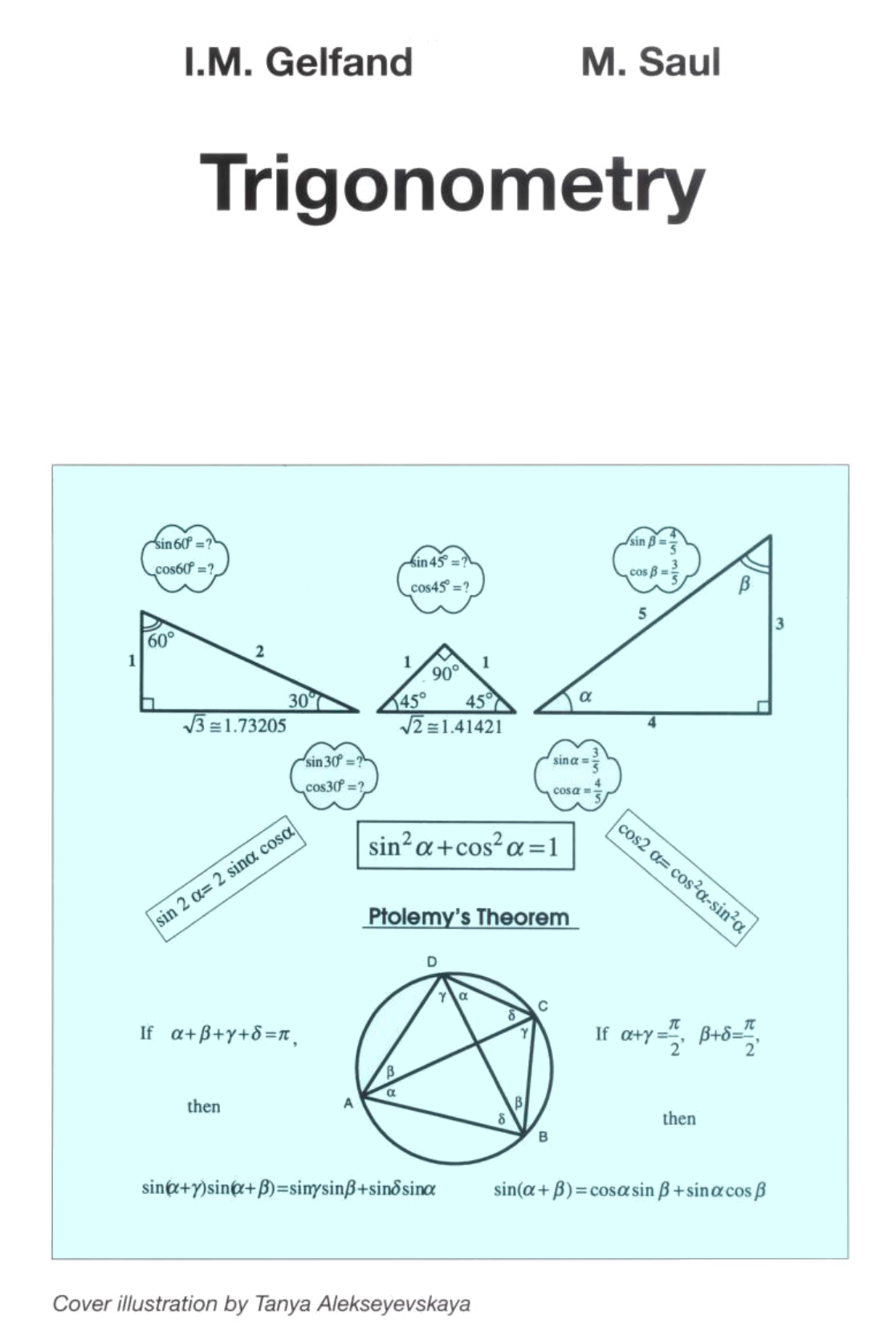
掌握三角函数的基本性质和应用，了解三角函数作为一种「数学工具」的意义。初步了解函数的抽象意义，以及函数图形的一些一般性质。掌握基本的解析几何，初步了解代数和几何的联系。
内容
- 三角函数
- 函数和图形
- 解析几何初步
课本
- Trigonometry, I. M. Gelfand and M. Saul
- Functions and Graphs, I. M. Gelfand, E. G. Glagoleva, and E. E. Shnol
- Basic Mathematics, Serge Lang
建议学生程度
九年级
力学I
课程简介
牛顿力学是现代物理学的起点，也应该作为学生学习物理的起点。这门课从知识结构而不是知识点出发讲授牛顿力学的基本理论。在讲授牛顿力学前，我们会引入必要的基础知识，如静力学等。
内容
- 静力学
- 运动
- 牛顿定律
课本
- Fundamentals of Physics: Mechanics, Relativity, and Thermodynamics, R. Shankar
建议学生程度
九年级
力学II
课程简介
作为力学I的延伸，力学II将引入基本的物理概念：动量和能量。在对这些物理概念的辨析中，学生将了解物理和数学的联系与区别。
内容
- 动量
- 能量
- 转动系统和角动量
- 谐振子
课本
- Fundamentals of Physics: Mechanics, Relativity, and Thermodynamics, R. Shankar
建议学生程度
十年级
解题策略
课程简介
如何解题是一个同时困扰初学者和职业数学家的问题。这门课将告诉学生解题不止需要熟练和投入，还需要进行策略性的思考。而这种策略性思考，和通常的「解题技巧」并不是一回事。通过这门课的学习，学生将体会「智力」和「智慧」的微妙区别，学习如何更成熟地解决问题。
内容
- 解题的一般策略
- 启发词典（实例）
课本
- How To Solve It, George Pólya
建议学生程度
十年级
逻辑基础
课程简介
自我矛盾是痛苦的来源之一，数学家的痛苦随着近几十年逻辑理论的发展减轻不少。不仅数学，现代逻辑学在计算机科学中也有广泛的应用。因为无处不在的应用，对基本逻辑的学习不仅必要，而且「经济」。通过这门课的学习，学生将了解基本逻辑思维的范式，清晰因逻辑结构产生的复杂性。
内容
- 命题逻辑的基本概念
- 证明策略
课本
- How To Prove It, Daniel J. Velleman
建议学生程度
十年级